When dealing with Unicode strings, you often need to get character properties: character category (letter, digit, mark, etc.), its lowercase and uppercase counterparts, shifts for Boyer-Moore algorithm, and so on. There are about one million characters in Unicode, so an array indexed by the character value would take too much space.
The property values often repeat themselves, for example, all Chinese characters have the same value of script and category. Using the specifically designed algorithm, we can compress the repetitions without sacrificing performance. However, many programmers failed to find a good solution to this task.
Suboptimal solutions
- Chapter 5 in Beautiful code demonstrates using a long switch or series of if statements to check whether the Unicode character is a letter or a digit. Something like that:
switch(ch) {
case 'a': return true;
case 'b': return true;
case 'c': return true;
case 'd': return true;
// ...
case 'z': return true;
case '{': return false;
case '|': return false;
case '}': return false;
case '~': return false;
// another 65 409 cases...
}
(As Ace witty noted, this function should belong to The Daily WTF, not to Beautiful code.) The author's final solution is a 64K table with character properties, which is bloated and just wrong, because Unicode has more than 65536 characters.
Multi-stage table
The optimal solution is O(1); it requires just 6 instructions on x86, without any branches or slow instructions. It's called a two-stage table.
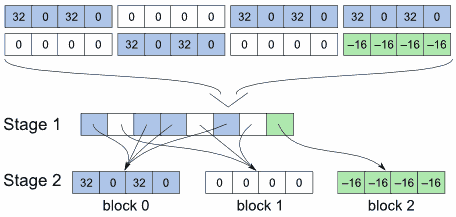
Assume there is an array of character properties (32, 0, 32, 0, 0, 0, ..., -16). To compress them, you can separate the array into blocks. For performance reasons, the block size should be a power of 2 (in this example, it is four).
When creating the table, the program eliminates the repeating blocks and place only the unique blocks in the second stage table. The first stage table contains pointers to these unique blocks. Often, the first stage items point to the same block, so the data is effectively compressed. For example, all blocks with values (32, 0, 32, 0) are replaced by pointers to the block 0 containing these values.
In practice, you should store the number of a unique block, not the pointer, in the first stage table, because the former takes less space. The second stage table is implemented as an array divided into fixed-size blocks.
The code to look up the table takes just three lines:
unsigned get_property(unsigned ch)
{
const unsigned BLOCK_SIZE = 256;
unsigned block_offset = stage1[ch / BLOCK_SIZE] * BLOCK_SIZE;
return stage2[block_offset + ch % BLOCK_SIZE];
}
A script to create the table
The Python script below creates the table. It avoids building an intermediate table with all characters; only the current block is kept in memory. The smallest possible data type for the table items is automatically chosen. The script builds the table for Unicode category, but it can be easily adapted to another property (just change __decode method and def_val constant in UnicodeDataExtractor).
Download the script for building multistage tables
Starting from version 7.8, PCRE includes a multi-stage table implementation based on this script.
A similar script in used in Python source code. Their script combines several character properties (category, combining class, and bidirectional info) into one table and automatically finds the value of block size yielding the smallest table. Python interpreter uses two-stage tables for the functions in unicodedata module and string.upper() / lower() functions.
Conclusion
Unicode standard explicitly recommends using two-stage tables (see chapter 5.1). So, the moral is to read the standard and follow it instead of trying to reinvent the wheel, as some programmers mentioned above did.

32 comments
I have an idea for which I don't expect that it can give better results in this case, but I've had an idea: imagine using a little smaller blocks, and such that the start of the block can be anywhere in the bigger table and not only at equally spaced points. To build the resulting tables, I believe that for searching for the subblock anywhere inside of the already formed bigger table some of the algorithms used in compression algorithms can be used. It would be interesting to try.
P.S. Congratulations -- your article is at the moment the most relevant on the web on the subject of two stage tables. I've tried to search for "two-stage table" and the biggest search site returns your article as the first match (I ho. Other don't know about it but give in matches or as sponsored links "Shop for a Table for two" and "Buy a Table for two at ..."
In the cases where the codepoint attribute is a bool, somethine like a BDD (binary decision diagram) or a perfect hash might work without a table.
Ace probably means not variable-sized blocks, but the blocks that can start at offsets not divisible by block size. In this case, you will have to store the full offset instead of the block number, so the first stage table will require a larger data type (e.g., unsigned short instead of unsigned char).
It's still an interesting idea. Thank you, Ace!
If you need to store several properties (e.g., script and category), you can save space by combining them into one table. Python creates the third table ("database record") storing all unique combinations of the properties; a two-stage table contains the offset in this table. Such table will be more compact, because all properties are more or less correlated.
I recently tried a three-stage table; it's much smaller, too.
Right.
> so the first stage table will require a larger data type (e.g., unsigned short instead of unsigned char).
Yes, that's why I expressed doubt (albeit the whole message was confusing as the result of careless editing) if it would work, since increasing the size of the first table pays off only if there are significantly less new tables introduced compared to the simplest solution.
However it's still an interesting theme for experiments. In such a setup, in the cases where some existing subtable doesn't already overlap at the start with another it would allow adding prefix to it (inserting something inside of the resulting table) in order to minimize the resulting table.
Speaking of Unicode, I was wondering what's the proper way of converting the hash functions you've been discussing to work with Unicode strings.
The subtlety is related to a problem you might have for comparing Unicode strings for equality, since Unicode has the notion of equivalent (and compatible) character sequences and normalization.
http://en.wikipedia.org/wiki/Unicode_normalization
There are lots of tricky things about Unicode and multi-byte encodings...
A multiplicative hash function will give you a better result if you process the string by characters (wchar_t), not by bytes. Small multipliers should still work nicely, because most users will use only the letters of their language, so the range of unique characters will be small. (Notable exceptions are ideographic and syllabic scripts, e.g., Chinese, Japanese, or Korean, which have a lot of unique characters.)
A more complex hash function such as Murmur or Paul Hsieh's function can be used without modification, as Won suggested.
speed size for Unicode 5.0 old algorithm 152 ticks per char 24 KB 2-stage 8 ticks per char 46 KB 3-stage 13 ticks per char 22 KBPhilip Hazel, the author of PCRE, chose the 2-stage table, which provides better performance at cost of twice larger memory usage. The patch will be included in the next version of PCRE.
Congratulations!
You can also employ the following very effective trick. There are many level-0 blocks (blocks containing the actual data) that contain all the same value (like Block 1 and Block 2 in your example). You do not have to store this entire block just so that you can later stuff pointers/indexes to it. Instead, you can store that repeated value in the higher-level stage(s) directly (if you can spare 1 bit to encode this pointer as "non-pointer").
This optimization can be used even more effectively with a higher-order staged tables, since the special "repeated" value can propogate even higher (for example, if level-1 stage block is full of the same "non-pointer" values, the block does not need to be created and, instead, the same "non-pointer" value can be stored in the stage above). The tables may detect "same-pointer" blocks in higher-order stages (not just leaf blocks), but this would require keeping more "extra" bits to distinguish "non-pointer" leaf data from "non-pointer" "skip-stage" pointers. So I did not do this in my attempts below.
My experience with a particular unicode subset ( U+000000 - U+10FFFF):
"original" 2-stage table. Size: 27648 bytes.
"optimized" 2-stage table. Size: 26112 bytes.
"optimized" 3-stage table. Size: 12112 bytes.
"optimized" 4-stage table. Size: 9632 bytes.
"optimized" 5-stage table. Size: 8208 bytes.
Sorry for the botched wiki formatting in the previous comment. Different wikis have different formatting rules. If someone can clean this up, it would be great.
Igor, thank you very much; it's an interesting idea. The table will be smaller, but you will have a branch (if statement) in your code, so it will be slower, because unpredictable branches are expensive on modern processors.
So, it's a time-space compromise (smaller table or faster code). If you want a smaller table, you could also explore data compression algorithms, especially RLE. The table can be uncompressed once (when your program starts up), then queried many times.
On another side, I fully agree that no normal application is not doing just one small task and then the cache pressure often becomes more important than the speed of the segment that was benchmarked with the full caches.
In Igor's case, the branch is very predictable. The jumps are short, forward jumps. Most of the time the branch target will be inside the current or next cache line. (Recall that the OP mentions 6 ops for a 2-stage table - this is *small* code.)
> the branch is very predictable
I'm very surprised to hear something like this. Can you please explain how would you predict what the next character to appear, not in hardware, but just as an algorithm or some statistical analysis? I'm still not able to imagine any predictor which would predict random jumps.
> Most of the time the branch target will be inside (...) cache line
That doesn't help if you have to wait the whole pipeline length because the target was not predicted. You'd lose 'length of the pipeline' T states. However I also think that if some code is used infrequently enough (so that the relevant cache entries are empty on the start) the "lighter on caches" algorithm has more chances to win.
Hi Peter,
I followed your explanation but probably I missed something because I didn't understand your multi-stage table.
The indexes of the array of characters properties you're talking about at the beginning of you article are the unicode code points?
Thanks for the answer!
I think I got it, let's resume without "optimization" tricks:
You build an array of character properties based on the .txt(s) from unicode org.
In a first instance the array length is 0x10FFFF. In your graph is called stage1.
After, you proceed subdividing the stage1 in fixed block size, 256 bytes, and since there are many
code point ranges with the same properties those blocks "perform" some sort of optimization.
Those blocks of properties go inside a second array called stage2.
Time by time you store a new block of properties inside stage2 you update stage1 with the relative pointers, better with the block number or you update stage1 with an existing block already computed.
After that you will have ranges of elements of stage1 repeated because the repetition properties of code points, and then you can compress the stage1 array and so reducing spaces.
All of this at "building" time, that is when you're going to build the two stage tables. Once finished you can simply store as normal array, stage1 and stage2, inside your code.
is it so?
If yes and if you have already done this what is the percentage of compression?
I meant if you're going to store the entire array of char properties for all code points and each element of the array is 4 bytes you will get about 4MB (0x10FFFF x 4) of spaces occupied while with your method?
Ace, the branch in question is a test for the magic bit -- "is it a pointer to the next block, or is it the data itself?" This branch will usually resolve the same and be very predictable.
What you are talking, I believe, is the expense of an extra level. Branch prediction has little to offer here, of course. However, it is important to see how many level will be triversed in the common case. It is possible (I did not check this) if the common case would not have to triverse all levels and, instead, would be optimized into higher-level blocks.
The article is crystal-clear but the comments are very confusing: where is the "if" statement and tests for "magic bit" in
unsigned get_property(unsigned ch) { return stage2[stage1[ch / BLOCK_SIZE] * BLOCK_SIZE + ch % BLOCK_SIZE]; } ???Axel, see this comment. In short: Igor has a different idea, which involves the "if" statement.
Oh OK I did not realize that your site did not display all comments by default. Reading from the middle on did not make any sense. Anyway I like your simpler 2-stage method better provided one can live with a 27K table.
Two-stage tables are pretty "sub-optimal" for space in many use cases. Not every program needs the full set of properties. Some just need to know e.g. all alphanumeric codepoints or all non-spacing marks, etc. With binary search that can be done with a 2-3 KiB interval table.
Making the distinction between O(log N) and O(1) here is almost completely irrelevant, since there's a constant, known upper bound for N. If your (relatively) massive table causes even a single, extra cache-line fill vs. the smaller table you've already lost, despite log(N) being 14 or so.
For binary search, you have to run a loop to look up in the interval table. For a multi-stage table, your lookup code is completely branchless (see the three lines above). It's a noticeable difference for modern processors with branch prediction.
PCRE and Boost authors decided to use my script. You can always run a benchmark to see which approach wins in your particular case.
> It's a noticeable difference for modern processors with branch prediction.
Most of the branches in a binary search loop *are* predictable though. It's a backwards branch forming a loop that's only going to break once -- either when it's exhausted the search or found a match. Saying something to the effect of "branch prediction bad" is not particularly insightful.
Also, a cacheline fill is an order of magnitude more expensive than a mispredicted branch. Unpredictable branches are certainly bad for performance, but it's gotten to the point where saying "hurrr branches bad" is just an overused meme without any sane quantification or analysis of what you're replacing it with.
That was supposed to be "branch [mis]prediction bad".
Frank, please feel free to do a benchmark
I'm not interested in doing artificial benchmarks on a whim, I just wanted to point out the insanity of this statement:
"The table will be smaller, but you will have a branch (if statement) in your code, so it will be slower, because unpredictable branches are expensive on modern processors."
A branch misprediction on "modern processors" costs about 16 cycles. In some situations that's a big deal -- but treating branches like some kind of unknown quantity, to be avoided at all costs, is a very weird phenomenon.
Especially when you're comparing it to something that adds tons of extra cache pressure, which won't even register in synthetic benchmarks but could easily destroy performance when you actually throw it into a real application.
The big switch in Beautiful Code Chapter 5 likely has fewer branches than you think.
The switch will be transformed into a lookup table (by the compiler) with many of the cases compressed in to one. Also every case returns to the same point.