Standard deviation is a statistic parameter that helps to estimate the dispersion of data series. It's usually calculated in two passes: first, you find a mean, and second, you calculate a square deviation of values from the mean:
double std_dev1(double a[], int n) {
if(n == 0)
return 0.0;
double sum = 0;
for(int i = 0; i < n; ++i)
sum += a[i];
double mean = sum / n;
double sq_diff_sum = 0;
for(int i = 0; i < n; ++i) {
double diff = a[i] - mean;
sq_diff_sum += diff * diff;
}
double variance = sq_diff_sum / n;
return sqrt(variance);
}
But you can do the same thing in one pass. Rewrite the formula in the following way:
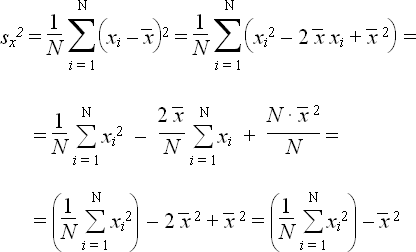
double std_dev2(double a[], int n) {
if(n == 0)
return 0.0;
double sum = 0;
double sq_sum = 0;
for(int i = 0; i < n; ++i) {
sum += a[i];
sq_sum += a[i] * a[i];
}
double mean = sum / n;
double variance = sq_sum / n - mean * mean;
return sqrt(variance);
}
Unfortunately, the result will be inaccurate when the array contains large numbers (see the comments below).
This trick is mentioned in an old Soviet book about programmable calculators (here is the reference for Russian readers: Финк Л. Папа, мама, я и микрокалькулятор. — М.: Радио и связь, 1988).

21 comments
Let's say each X is either (2**40)+1 or (2**40)-1 with probability 0.5. Two loop computation would yield a mean of 2**40 and correct stddev. One loop computation would produce incorrect stddev results.
If you happen to still have the book, "Финк Л. Папа, мама, я и микрокалькулятор", could you please scan and post it somewhere? I read this book when I was a kid. It had a great influence on me.
unfortunately, I don't own this book; I read it in a library about 10 years ago. It deeply influenced me, too.
I have just scanned the book in djvu format and and uploaded it to
http://www.arbinada.com/pmk/node/310
It is a great little book. Have fun.
Regards,
Greg W.
James, thank you for the link. This method looks interesting, but, if I understand correctly, it requires 2 divisions at every iteration, which is very slow. It's probably makes more sense to use the two-pass calculation. Still thanks for the info.
(It's probably not accidental that M. Hoemmen is PhD student on Berkeley, where Prof. W. Kahan is. And I wouldn't be surprised if James is there too. :) )
That simple example shows once again why Prof. W. Kahan designed the x87 FPU with the possibility to use 80 bits for partial results. But Microsoft intentionally designed compilers to ignore that feature (and more).
Well that's a good moment to visit again Prof. Kahan's web page
http://www.cs.berkeley.edu/~wkahan/
and also read, for example
Marketing versus Mathematics
http://www.cs.berkeley.edu/~wkahan/MktgMath.pdf
"Old Kernighan-Ritchie C works better than ANSI C or Java!"
"In 1980 we went to Microsoft to solicit language support for the 8087, for
which a socket was built into the then imminent IBM PC. Bill Gates attended
our meeting for a while and then prophesied that almost none of those sockets
would ever be filled! He departed, leaving a dark cloud over the discussions.
Microsoft’s languages still lack proper support for Intel’s floating-point."
or
http://www.cs.berkeley.edu/~wkahan/Math128/SqSqrts.pdf
"In particular Bill Gates Jr., Microsoft’s language expert, disparaged the extra-wide format in 1982 with consequences that persist today in Microsoft’s languages for the PC. Sun’s Bill Joy did likewise."
or
Floating-Point Arithmetic Besieged by “Business Decisions”
http://www.cs.berkeley.edu/~wkahan/ARITH_17.pdf
The first paper is from 2000 and I don't know if Java now has the extended precision floating point for partial results. Modern CPU instructions "for multimedia" of course don't. Which makes them potentially dangerous when used on formulas like the starting one.
Finally, from:
http://www.cs.berkeley.edu/~wkahan/Mindless.pdf
"Routine use of far more precision than deemed necessary by clever but numerically naive programmers, provided it does not run too slowly, is the best way available"
It does not require two divisions - only one.
// for sample variance double std_dev(double a[], int n) { if(n == 0) return 0.0; int i = 0; double meanSum = a[0]; double stdDevSum = 0.0; for(i = 1; i < n; ++i) { double stepSum = a[i] - meanSum; double stepMean = ((i - 1) * stepSum) / i; meanSum += stepMean; stdDevSum += stepMean * stepSum; } // for poulation variance: return sqrt(stdDevSum / elements); return sqrt(stdDevSum / (elements - 1)); }Arne, thank you for your algorithm. I've already seen similar algorithms but I don't know how they are derived. I'd greatly appreciate if you would point me to some source which explains derivation of this and/or similar algorithms. According to some experiments I made for some similar calculations the algorithms like the one you presented here give significantly better results compared to the "one pass, full squares" (which can produce even completely wrong results for "inconvenient" input) but they can still be noticeably less accurate than the real two pass algorithm. Do you know of any source where such error analysis is shown? Thank you.
But sometimes the input to sqrt can be negative, resulting in... well, who knows what, given that you're coding in C.
Try a list with 3 copies of 1.4592859018312442e+63 for example.
typedef struct statistics_s { size_t k; // sample count double Mk; // mean double Qk; // standard variance } statistics_t; static void statistics_record (statistics_t *stats, double x) { stats->k++; if (1 == stats->k) { stats->Mk = x; stats->Qk = 0; } else { double d = x - stats->Mk; // is actually xk - M_{k-1}, // as Mk was not yet updated stats->Qk += (stats->k-1)*d*d/stats->k; stats->Mk += d/stats->k; } } static double statistics_stdev (statistics_t *stats) { return sqrt (stats->Qk/stats->k); } static size_t statistics_nsamples (statistics_t *stats) { return stats->k; } static double statistics_variance (statistics_t *stats) { return stats->Qk / (stats->k - 1); } static double statistics_stdvar (statistics_t *stats) { return stats->Qk / stats->k; } static double statistics_init (statistics_t *stats) { stats->k = 0; }Knuth actually has one pass algorithm like this
_M gets you mean, _C / (N-1) is variance
I've come across a problem using this algorithm where the variance calculation step outputs a negative zero (in OpenCL). Then the standard deviation step becomes the sqrt of a negative number, which results in NaN.
It might be wise to use the absolute value of the variance to avoid this.
ammendes, thank you so much
Thank you! Your derivation saved me thinking!
If the variance calculation is changed to this:
Wouldn't that be accurate, always, even for large numbers? this assumes there is no overflow, of course.
And maybe this (slightly different arrangement) might help prevent some overflows:
Never mind, it looks like those are equivalent. Sorry.