Standard deviation is a statistic parameter that helps to estimate the dispersion of data series. It's usually calculated in two passes: first, you find a mean, and second, you calculate a square deviation of values from the mean:
double std_dev1(double a[], int n) {
if(n == 0)
return 0.0;
double sum = 0;
for(int i = 0; i < n; ++i)
sum += a[i];
double mean = sum / n;
double sq_diff_sum = 0;
for(int i = 0; i < n; ++i) {
double diff = a[i] - mean;
sq_diff_sum += diff * diff;
}
double variance = sq_diff_sum / n;
return sqrt(variance);
}
But you can do the same thing in one pass. Rewrite the formula in the following way:
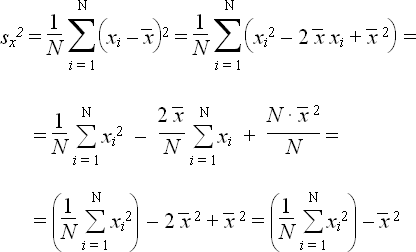
double std_dev2(double a[], int n) {
if(n == 0)
return 0.0;
double sum = 0;
double sq_sum = 0;
for(int i = 0; i < n; ++i) {
sum += a[i];
sq_sum += a[i] * a[i];
}
double mean = sum / n;
double variance = sq_sum / n - mean * mean;
return sqrt(variance);
}
Unfortunately, the result will be inaccurate when the array contains large numbers (see the comments below).
This trick is mentioned in an old Soviet book about programmable calculators (here is the reference for Russian readers: Финк Л. Папа, мама, я и микрокалькулятор. — М.: Радио и связь, 1988).
19 comments
Ten recent comments are shown below. Show all comments
Arne, thank you for your algorithm. I've already seen similar algorithms but I don't know how they are derived. I'd greatly appreciate if you would point me to some source which explains derivation of this and/or similar algorithms. According to some experiments I made for some similar calculations the algorithms like the one you presented here give significantly better results compared to the "one pass, full squares" (which can produce even completely wrong results for "inconvenient" input) but they can still be noticeably less accurate than the real two pass algorithm. Do you know of any source where such error analysis is shown? Thank you.
But sometimes the input to sqrt can be negative, resulting in... well, who knows what, given that you're coding in C.
Try a list with 3 copies of 1.4592859018312442e+63 for example.
typedef struct statistics_s { size_t k; // sample count double Mk; // mean double Qk; // standard variance } statistics_t; static void statistics_record (statistics_t *stats, double x) { stats->k++; if (1 == stats->k) { stats->Mk = x; stats->Qk = 0; } else { double d = x - stats->Mk; // is actually xk - M_{k-1}, // as Mk was not yet updated stats->Qk += (stats->k-1)*d*d/stats->k; stats->Mk += d/stats->k; } } static double statistics_stdev (statistics_t *stats) { return sqrt (stats->Qk/stats->k); } static size_t statistics_nsamples (statistics_t *stats) { return stats->k; } static double statistics_variance (statistics_t *stats) { return stats->Qk / (stats->k - 1); } static double statistics_stdvar (statistics_t *stats) { return stats->Qk / stats->k; } static double statistics_init (statistics_t *stats) { stats->k = 0; }Knuth actually has one pass algorithm like this
_M gets you mean, _C / (N-1) is variance
I've come across a problem using this algorithm where the variance calculation step outputs a negative zero (in OpenCL). Then the standard deviation step becomes the sqrt of a negative number, which results in NaN.
It might be wise to use the absolute value of the variance to avoid this.
ammendes, thank you so much
Thank you! Your derivation saved me thinking!